11 min to read

能写的都写完了

Featured image

从KMP到AC自动机

一，前言

本篇文章主要介绍有关字符串匹配的算法知识，详细讲解KMP，字典树，AC自动机，这三个算法。为了方便讲解，其中ac自动机的部分只是KMP和字典树的结合体，其中涉及有限状态机的部分，由于篇幅有限，暂不论述（）

·

二，KMP算法

2.1字符串匹配

现在我们来复习一下字符串匹配：

问题：已知到两个字符串t，s（t<s）找到t在s中第一次出现的位置信息。那么我们应该如何去做呢？

BF:最简单的就是bf算法，即朴素算法，那么到底有多朴素呢？就是一个一个字符串进行单字符的匹配，如果相同，则继续匹配，如果不同，则从最开始匹配的字符多对应的后一个字符重新开始匹配。那么，最终的时间复杂度最坏为O(mn)。

KMP:下面，我们来进行优化，首先找到BF算法中所浪费的时间。经过我们仔细的分析发现当单个字符不同时，s，t字符串从头匹配，那么在这一过程中，我们可以通过数学计算，推断出那些匹配一定是错误的，从而避免这些多余的匹配。

2.2 KMP算法

按照这个思路，两位大师发明了一个名为KMP的算法，在这一算法中他们找到了其中避免多余匹配的数学计算方法———next数组。

我们来看一下下面一些字符所对应的next数组：模式串t对应

数组序号    0    1    2    3    4    5    6    7

字符串        a    a    a    a    a    a    a    a

next数组    -1   0    1    2    3    4    5    6

数组序号    0    1    2    3    4    5    6    7

字符串        a    b    c    d    e    f    g    h

next数组    -1   0    0    0    0    0    0    0

数组序号    0    1    2    3    4    5    6    7    8   

字符串        a    b    c    a    a    b    a    b    c

next数组    -1   0    0    0    1    1    2    1    2

我们先熟悉一下next数组的结构，然后理解其背后的原理。next数组的主要功能用一句话来说就是最优化回溯，在bf算法中，回溯的方式非常的简答粗暴，直接选择从开始匹配节点回溯，这样会产生不必要的匹配。而next数组，则是仅对模式串t（t<s）进行回溯操作，而主串s（t<s）则是不断前进，最终实现时间复杂度为O(m+n)。

实质上：这里的next[i]指向的是当第i个字符串发生失配（匹配失败）时，需要转跳的位置。

之后我们将结合字典树将这一思想应用到ac自动机上

其中以第3组数据为例，进行具体分析

第一步：初始化

将next数组初始值设置为-1

第二步：找到最优回溯点（1）–双指针

分析一下next数组的构造逻辑，我们就可以得出一定要使用双指针进行操作，一个不断前进，一个用于储存fail信息（即匹配失败时需要回溯到的位置）。

所以定义：

  1. i为遍历模式串指针，初始设为0

  2. k为储存fail信息指针，初始设为-1

第三步：找到最优回溯点（2）–循环体

 我们用i遍历模式串的过程中，不断地与t[k]进行比较。

我么需要知道以下两点：\rhdk的本质—-储存字符i的失配信息（即当i匹配失败时，模式串将回溯到k位置）\rhd当a[i]和a[k]匹配成功时，所求的是next[i+1]的信息，而不是next[i];

·

那么在遍历模式串t过程中：

最终实现的代码如下:

vector<int> getnext(string t)
{
    int i=0,k=-1;
    vector<int> next(t.size());
    next[0] = -1;
    //注意这里是size-1，在每一次循环体中获得的是next[i+1]
    while(i<t.size()-1)
    {
        if (k == -1 || t[i] == t[k])
        {
            i++;
            k++;
            next[i] = k;
        }
        else
            k = next[k];
    }
    return next;
}

同时这里提供对应的匹配的代码：其中s是主字符串，t为模式串，函数返回t在s中第一次出现的位置。

int kmp(string s, string t)
{
    vector<int> next = getnext(t);
    for (auto x : next)cout << x << " ";
    int i = 0;
    int j = 0;

    while (i < (int)s.size() && j < (int)t.size())
    {
        if (j == -1 || s[i] == t[j])
        {
            i++;
            j++;
        }
        else
        {
            j = next[j];
        }
    }

    if (j == t.size())
        return i - j; // 首次出现的位置
    return -1; // 未找到
}

三,字典树

3.1字典树的背景：

引入：之前所提到的字符串匹配算法，如kmp，bp等他们都只能进行单个模式串匹配，即一段文本s，一个模式串t，找到t在s中的位置。但是，如果同时有多个t呢？我们可以用单模式匹配一个一个进行处理，但是这显然不是最优的选择。基于这个问题——多模式匹配（一段文本中同时查找多个模式字符串集合的匹配位置），字典树横空出世。

字典树的概念由多位学者在不同的时间提出的。Emil Thoman Dijkstra 在 1959 年的一篇论文中首次提出了 Trie 的概念，但并没有广泛传播。Edward Fredkin 在 1960 年代早期独立提出了 Trie 结构，并在他的一些论文中使用了这个术语。之后字典树逐渐被后人所完善和改进，最终得到广泛地应用于多模式匹配等问题中。

3.2字典树介绍：

3.2.1 Brief Overview

总的来说，字典树是处理多模式匹配的一种数据结构，其中每个叶子节点代表一个要匹配的模式。然后，通过遍历文本并在字典树中进行匹配，可以高效地找到文本中出现的所有模式。

为了更好的理解字典树，我们先来看一张图片：

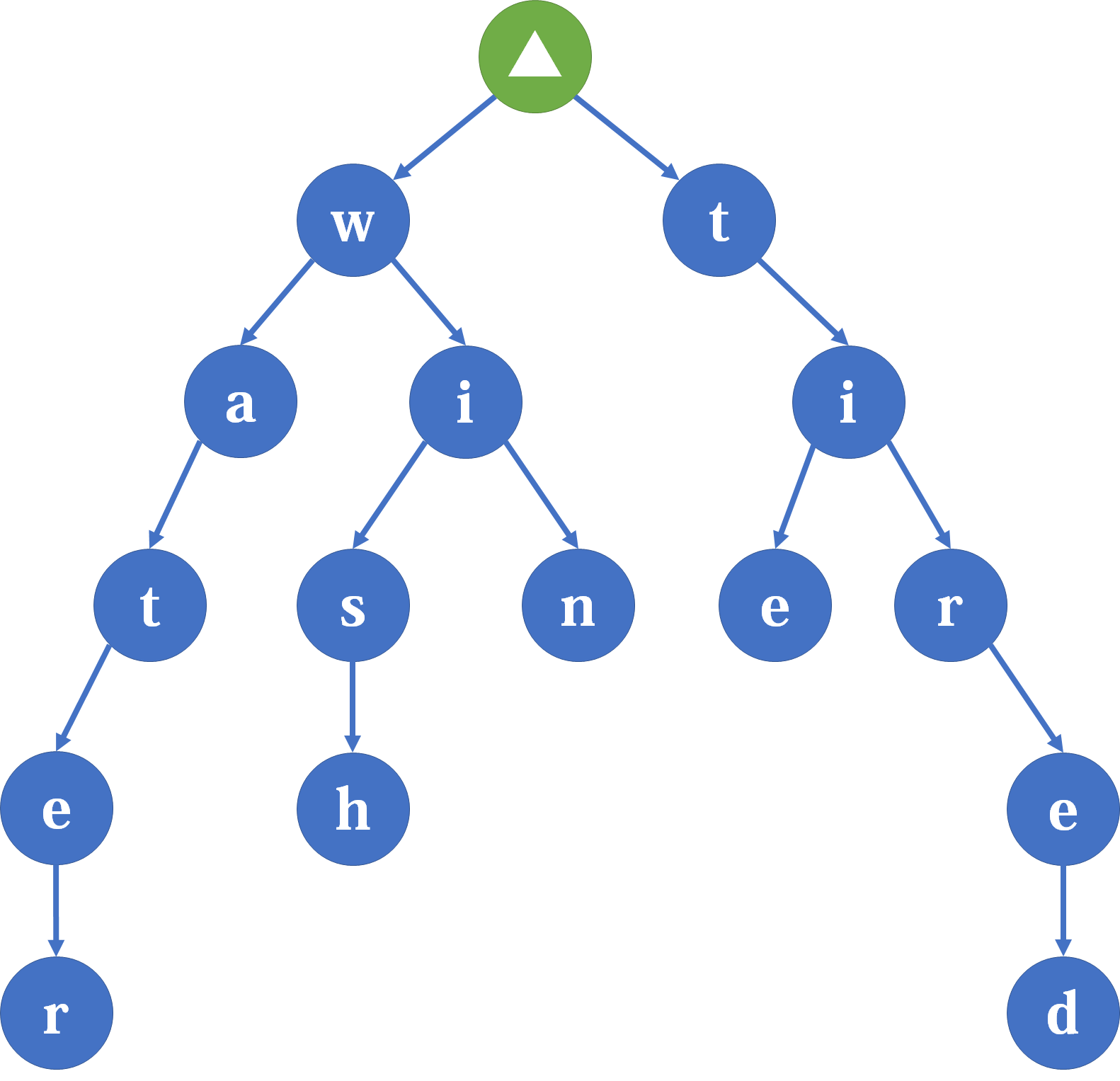
其中，绿色箭头代表着匹配开始的阶段，即匹配的初始位置。后面连接着一个一个字母，其中相互连接的字母构成了一个单词（即模式串）。以这张图为例，其中所蕴含的模式串有很多。比如从w开始，向下延伸，连接形成water，win，wish。蕴含的模式串并不局限于这些，以w开头的模式串还可以是wat，wis，wa等等。只需要在相应节点处加上终止符即可，表明到此处已经成功匹配到一个模式串。

3.2.2 Principle Analysis

在单模式匹配中，我们只需对着一个模式串依次遍历即可。但是到了多模式匹配，我们要设计一种可以同时遍历这些模式串的一个结构，这个结构就是字典树。它将所有的模式串相关联起来，这种关联方式借助了前缀的原理。举一个例子：abcdef的前缀可以是ab，abc，abcd。字典树将每一个模式串分解为一个个字符，寻找相同的前缀，并通过树的方式统一起来。So：字典树==前缀和+有根树。

在匹配时，每读取一个主串的字符，都会将其输入到字典树中，如果匹配成功，那么匹配的指针向后移，当指针指向的节点带有终止符时，说明成功匹配一个模式串。利用前缀和，字典树，可以立刻寻找一个新的模式串，该模式串的前缀是成功匹配的模式串。如此以来，字典树便可以同时处理多个模式串的匹配问题了。

3.2.3 Detailed Procedures

这里介绍一个具体的应用:单词查询

（这里不写模式匹配算法的原因：文章之后要结合kmp，进化成ac自动机解决模式匹配的问题。若只用字典树解决模式匹配，也可以利用字典树+BF暴力解决）

input：若干个单词，插入进字典树中。

output：然后输入一个单词，查询该单词这个字典中出现的次数。

1.构造：

node:

node*ch[k]:每一个节点实际上都有26个指针，分别对应着的26个字母。ep.开始ch[k]全为空，当该节点对应下一个字符为26个字母之一，ch[26个字母之一]指向一个新的node。

count:

count用来表示匹配到当前节点时，有count个模式串匹配成功

#include<bits/stdc++.h>
using namespace std;
#define K 26

struct node
{
    node* ch[K];
    int count;
    node() {
        memset(ch, NULL, sizeof(ch));
        count = 0;
    }
};

node* root=new node;

向该字典树中，增添新的模式串str

void insert(string str)
{
    node* t = root;
    int len = str.length();
    for (int i = 0; i < len; i++)
    {
        //获得下一个字符
        int x = str[i] - 'a';
        //建立下一个字符对应的路径，如果没有，则新建
        if (t->ch[x] == NULL) {
            t->ch[x] = new node;
        }
        //建立路径
        t = t->ch[x];
    }
    //模式串在当前节点匹配完成
    t->count++;
}

2.查询和使用：

int find(string t) {
    node* p = root;
    for (int i = 0; t[i]; ++i) {
        //不匹配，返回0,为没有找到。
        if (p->ch[t[i]-'a']==NULL) return 0;
        //当前节点匹配，p到下一个节点
        p = p->ch[t[i]-'a'];
    }
    return p->count;
}

//该功能只能实现对单词的查询，不是模式匹配。
int main() {
    int m;
    cin >> m;
    while (m--) {
        char op;
        string s;
        cin >> op;
        if (op == 'I') {
            cin >> s;
            insert(s);
        }
        if(op=='Q'){
            cin >> s;
            cout << find(s) << endl;
        }
    }
    return 0;
}

将所有代码复制到IDE中就可以执行了，这里给出测试数据

Input：

7

I water

I win

I wish

I tie

I tied

Q win

Q tiede

output:

1

0

四,AC自动机

通过之前的学习可以发现，kmp可以在线性时间内解决单模式匹配问题，而字典树可以解决多模式匹配问题，但是每一次失败都需要进行回溯（字符串匹配BP算法）。

所以为了在线性时间内解决多模式匹配的问题，设计了AC自动机=Trie树+kmp。

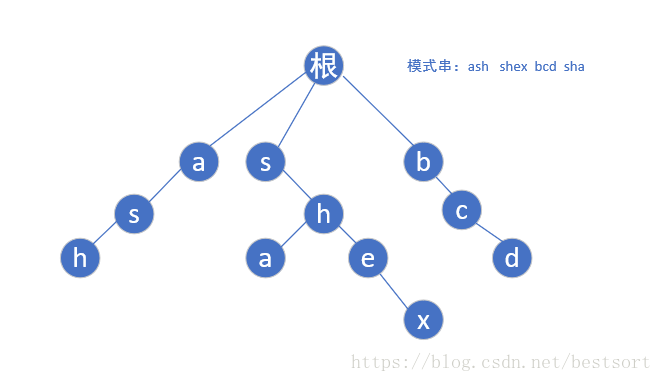
这里我们还是借用一个AC自动机经典的图片进行讲解：

如图，这是一个字典树，储存的模式串有ash，sha，shex，bcd。现在给你一个文本，写一个函数返回文本中这些单词出现的。

在深入了解了KMP中的next数组之后，进行下面的阅读：

我们可以直到，next数组是指S[i]和T[j]不同时，j应该回退的位置。那么AC自动机也是如此，其在字典树的基础上加上了一个失配指针（fail指针）。fail指针的功能是指向匹配失败后转跳的位置，所以在字典树构造完成后，再给每一个节点加上一个失配指针，AC自动机就构造完成了。我们来看字典树添加失配指针后的图解：

那么如何添加失配指针呢？我们先来分析一下失配指针的几个特性：

结合者两个特性我们可以按照以下过程添加失配指针，由于fail指针都是向上走的。我们可以进行从root节点开始进行广度优先搜索。具体过程如下：

  1. 树根入队

  2. 若队列不为空，则取对头元素t并出队，访问该元素的每一个子节点（对应为26个字母）

  • 若子节点不为空，则子节点失配指针指向该节点的失配指针，即t->ch[i]->fail=t->fail->ch[i]同时子节点入队。

  • 若子节点为空，则子节点指向该节点的fail指针对应的子节点，即t->ch[i]=t->fail->ch[i]

    3.队列为空时，算法结束。

代码如下：

void build_ac()
{
    queue<node*> q;
    root->fail = root;
    q.push(root);
    while (!q.empty())
    {
        node* t;
        t = q.front();
        q.pop();
        for (int i = 0; i < K; i++)
        {    
            if (t->ch[i])
            {
                if (t == root) t->ch[i]->fail = root;
                else
                t->ch[i]->fail = t->fail->ch[i];
                q.push(t->ch[i]);
            }
            else
            {
                if (t->fail == root)t->ch[i] = root;
                else
                t->ch[i] = t->fail->ch[i];
            }
        }
    }
}

模式匹配：

从树根开始处理模式串的每个字符，沿着当前字符的fail指针遍历。在遍历的过程中类似字典树的处理方式，统计每一个节点的count值（终止符，单词个数等等），即可计算一系列与模式匹配有关的搜索结果。这里我们演示统计主串种含模式串的个数，即出现的单词数。

代码如下:

int query(string str)
{
    int ans = 0;
    node* t = root;
    int len = str.length();
    for (int i = 0; i < len; i++)
    {
        int x = str[i] - 'a';
        t = t->ch[x];
        for (node* u = t; ~u->count;u=u->fail)
        {
            ans += u->count;
            u->count = -1;
        }
    }
    return ans;
}

加上预先构建好的字典树，就完成AC自动机的所有内容了，下面是完整代码：

#include<bits/stdc++.h>
using namespace std;
#define K 26

struct node
{
    node* fail;
    node* ch[K];
    int count;
    node() {
        fail =NULL;
        memset(ch, NULL, sizeof(ch));
        count = 0;
    }
};

node * root;
//字典树构建
void insert(string str)
{
    node* t = root;
    int len = str.length();
    for (int i = 0; i < len; i++)
    {
        int x = str[i] - 'a';
        if (t->ch[x] == NULL) {
            t->ch[x] = new node;
        }
        t = t->ch[x];
    }
    t->count++;
}
//AC自动机构建
void build_ac()
{
    queue<node*> q;
    root->fail = root;
    q.push(root);
    while (!q.empty())
    {
        node* t;
        t = q.front();
        q.pop();
        for (int i = 0; i < K; i++)
        {    
            //如果对应的子节点不为空
            if (t->ch[i])
            {    
                //这里对根节点进行特殊处理
                if (t == root) t->ch[i]->fail = root;
                else
                t->ch[i]->fail = t->fail->ch[i];
                q.push(t->ch[i]);
            }
            else
            {
                if (t->fail == root)t->ch[i] = root;
                else
                t->ch[i] = t->fail->ch[i];
            }
        }
    }
}
//多模式匹配：单词个数查询
int query(string str)
{
    int ans = 0;
    node* t = root;
    int len = str.length();
    for (int i = 0; i < len; i++)
    {
        int x = str[i] - 'a';
        t = t->ch[x];
        //沿fail树进行遍历
        for (node* u = t; ~u->count;u=u->fail)
        {
            //统计单词个数
            ans += u->count;
            u->count = -1;
        }
    }
    return ans;
}

int main()
{
    root = new node;
    int n; cin >> n;
    while (n--)
    {
        string x;
        cin >> x;
        insert(x);
    }
    build_ac();
    string s; cin >> s;
    cout << query(s)<<endl;
}

·